
You can open the diary file in a text editor. Optionally, you can give the name of the log file, say − The diary function creates an exact copy of your session in a disk file, excluding graphics. MATLAB executes the above statements and displays the following result.
MATLAB POLYTOOL EXPORT CODE
Create a script file and type the following code − The following example demonstrates the concept. Where, my_data.out is the delimited ASCII data file created, num_array is a numeric array and dlm_char is the delimiter character. Syntax for using the dlmwrite function is −ĭlmwrite('my_data.out', num_array, 'dlm_char') Where, my_data.out is the delimited ASCII data file created, num_array is a numeric array and −ascii is the specifier. Using the save function and specifying the -ascii qualifier There are two ways to export a numeric array as a delimited ASCII data file − MEX-file to access your C/C++ or Fortran routine that writes to a particular text file format.Īpart from this, you can also export data to spreadsheets. Specialized ASCII file using low-level functions such as fprintf. Rectangular, delimited ASCII data file from an array.ĭiary (or log) file of keystrokes and the resulting text output. You can create the following type of files − For this, MATLAB provides several data export options. MATLAB allows you to use your data in another application that reads ASCII files. The data at both ends of the plot tracks the fitted curve.Data export (or output) in MATLAB means to write into files. The confidence bounds are closer together indicating that there is less uncertainty in prediction. This graph shows a much better fit to the data. Then, drag the vertical reference line to the x-value of 2 (or type 2 in the X Values text box). In the Degree box at the top, type 3 for a cubic model. The two points to the right are dragging down the estimate of the slope. The bulk of the data with x-values between zero and two has a steeper slope than the fitted line. If you do not specify the degree of the polynomial, polytool does a linear fit to the data. The variables x1 and y1 are data points from the "true" function without error. The variables x and y are observations made with error from a cubic polynomial. To start the demonstration, you must first load the data set. You can use polytool to do curve fitting and prediction for any set of x-y data, but, for the sake of demonstration, the Statistics Toolbox provides a data set ( polydata.mat) to teach some basic concepts. An Export list box to store fit results into variables.
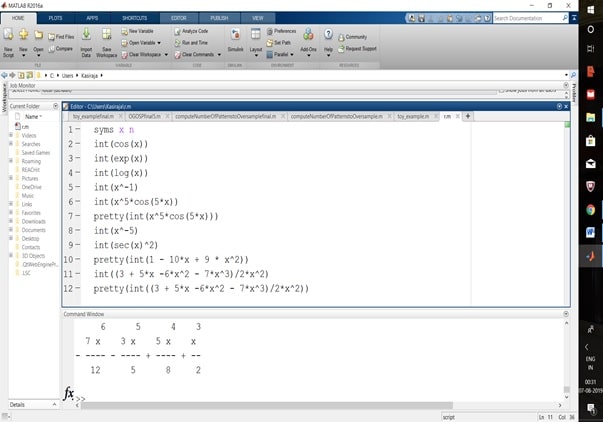
A Close button to end the demonstration.Bounds and Method menus to control the confidence bounds and choose between least squares or robust fitting.A draggable vertical reference line to do interactive evaluation of the polynomial at varying x-values.


 0 kommentar(er)
0 kommentar(er)
